1318. Толстая монета
 Вид в окрестностях
Дюссельдорфа. 1865. Окончив
в 1860 году Петербургскую Академию художеств с большой золотой медалью, Иван
Шишкин получил право на поездку за границу. В 1861—1865 годах молодой художник
странствовал по Европе, где посещал мастерские известных художников.
Вид в окрестностях
Дюссельдорфа. 1865. Окончив
в 1860 году Петербургскую Академию художеств с большой золотой медалью, Иван
Шишкин получил право на поездку за границу. В 1861—1865 годах молодой художник
странствовал по Европе, где посещал мастерские известных художников.
По заказу Н.Д. Быкова он написал в 1865
году картину «Вид окрестностей Дюссельдорфа», за которую получил звание
академика.
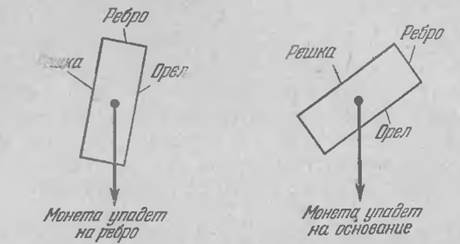
В городе N люди настолько полюбили
игру с монетой, что двух исходов (орел, решка) им оказалось мало. Поэтому
решено было создать толстую монету, одним из исходов бросания которой было бы
падение на ребро.
Какую наименьшую толщину должна иметь
монета радиуса r, чтобы вероятность
ее падения на ребро равнялась 1/n?
Считать, что монета имеет вид прямого кругового цилиндра, а поверхность, на
которую она бросается, является клейкой (монета, коснувшись поверхности, падает
на ребро или на одно из оснований).
Вход. Каждая
строка является отдельным тестом и содержит целочисленный радиус монеты r (0 < r < 100000) и целое значение n
(1 < n < 100).
Выход. Для
каждого теста в отдельной строке вывести искомую наименьшую толщину монеты.
Результат выводить с точностью до 6 десятичных знаков.
|
Пример входа |
Пример выхода |
|
1 3 100 20 1000 50 |
0.707107 10.012523 40.008002 |
РЕШЕНИЕ
теория
вероятности
Анализ алгоритма
Рассмотрим монету как вписанную в
сферу, центр которой совпадает с центром тяжести монеты. Считаем, что
поверхность, на которую бросается монета, является клейкой.
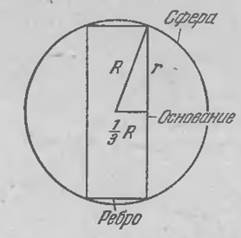
Лемма.
Поверхность куска сферы, заключенного между двумя параллельными плоскостями,
пропорциональна расстоянию между этими плоскостями. Поэтому толщина нашей
монеты должна составлять 1 / n
диаметра сферы (на рисунке показан случай n
= 3).
Доказательство. Площадь сферы равна 4πR2.
Площадь поверхности шарового сегмента равна S = 2πRH, где R – радиус шара,
H – его высота. Пусть расстояние от центра сферы до одной из параллельных
плоскостей равно d. Тогда площади поверхностей боковых шаровых сегментов
равны S = 2πR (R – d). Площадь поверхности сферы, заключенной между
параллельными плоскостями, равна 4πR2 – 2*2πR (R – d)
= 4πRd.
Вероятность того, что монета упадет
на ребро, равно отношению площади поверхности сферы, заключенной между
параллельными плоскостями, к площади поверхности всей сферы. То есть ![]() . Или то же самое что и
. Или то же самое что и ![]() . Откуда d = R / n. То есть толщина монеты
должна составлять 1 / n диаметра
сферы.
. Откуда d = R / n. То есть толщина монеты
должна составлять 1 / n диаметра
сферы.
Пусть R – радиус сферы, а r – радиус монеты. По теореме Пифагора
![]()
или
![]() ,
, ![]() ,
, ![]()
Откуда искомая толщина монеты должна
быть как минимум
2 * ![]() =
= ![]()
Реализация алгоритма
Читаем входные данные, вычисляем
искомую толщину монеты и выводим ее.
while(scanf("%lf
%lf",&r,&n) == 2)
{
res = r /
sqrt(n*n-1)*2;
printf("%.6lf\n",res);
}